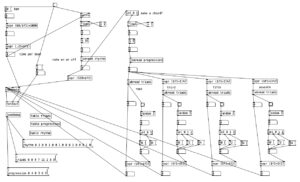
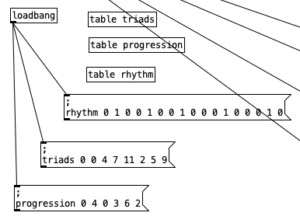
In the previous post we looked at a random arpeggiator that uses diatonic chord progressions. In this entry we will be using the same technique for creating diatonic chord progressions, but we will be applying it to create block seventh chords that repeat in a sequencer like fashion. Again we use the same code used in the scale sequencer to translate tempo from beats per minute to time per beat (expressed in milliseconds). As mentioned, we use the same table, ; triads 0 0 4 7 11 2 5 9, from the previous post to denote the notes of C Major, arranged as stacked thirds.
As we did in the previous patch, we can make a list of index numbers that relate to the triads table, which can be used to define the roots of a chord progression. In this case we are using the table ; progression 0 4 0 3 6 2. This results in the progression Dm7, CMaj7, Bm7(b5), Am7, G7. The other new element of this patch involves introducing a rhythmic pattern. This is accomplished using the table rhythm, where we use 1 to indicate a chord happening, and 0 to mean a rest happening. The table includes 16 numbers, indicating a single measure of sixteenth notes. The resulting rhythm starts out using syncopation where the first three chord jabs occur once every three sixteenth notes (or a dotted eighth note). The final two chords occur on the off beats of beats three and four, yielding a pleasantly funky rhythm.
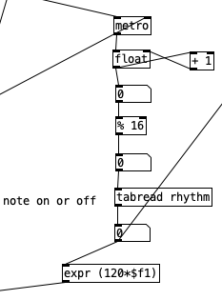
We use the rhythm table table in a very simple manner. We mod the counter to 16, resulting in a sixteenth note rhythm that repeats every measure. We then read the rhythm table. Multiplying that number, which will be a zero or a one, by 120 gives us a velocity. A velocity of zero results in makenote not generating a note, while the chord stabs will be reasonably loud at 120.
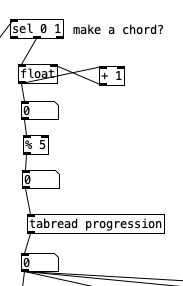
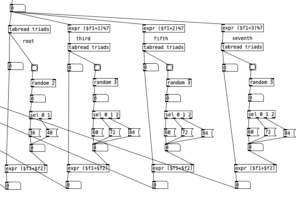
The number from tabread rhythm is then also passed to a sel statement. Remember that this note will only be a zero or a one. Thus, by using sel 0 1, and only using the outlet for 1, we only pass to the rest of the algorithm when a chord is supposed to occur. We then have a counter that is for the current chord, modding that to 5 gives us an index for reading the progression table.
The output of tabread progression then in turn feeds four similar parallel algorithms that generate the specific notes of the given chord. These four algorithms are laid out left to right, and correspond to the root, third, fifth, and seventh of the given chord. In case of the root, the output of tabread progression and uses it as the input to tabread triads, which will yield the root of the triad. This is also added to one of two random octaves, 36 or 48 which will yield a note in the bass clef.
The other three notes add a number to the output of tabread progression. These numbers, one, two, and three, correspond to the third, fifth, and seventh of the chord. Modding that number by seven wraps any number that goes beyond the length of the table back to the beginning. The output of those expr statements then feeds tabread triads, yielding specific pitches. These pitches are added to one of three random octaves, 60, 72, or 84 to get random voicings. All four outputs of the expr statements, which give the transposed MIDI note numbers of the root, third, fifth, and seventh are fed to makenote which creates the chord when it is fed a velocity of 120. The output of this patch sounds like this . . .