It has been a busy month for me, so I’m afraid this experiment is not as challenging as it could be. I used the Organelle patch Constant Gardener to process sound from my lap steel guitar. This patch uses a phase vocoder, which allows the user to control speed and pitch of audio independently from each other. While I won’t go into great detail about what a phase vocoder is and how it works, it uses a fast Fourier transform algorithm to analyze an audio signal and to reinterpret it as time-frequency representation.
This process is dependent upon the Fourier analysis. The idea behind Fourier analysis is that complex functions can be represented as a sum of simpler functions. In audio this idea is used to separate complex audio signals into its constituent sine wave components. This idea is central to the concept of additive synthesis, which is based upon the idea that any sound, no matter how complex, can be represented by a number of sine wave elements that can be summed together. When we convert an audio signal to a time-frequency representation we get a three-dimensional analysis of the sound where one dimension is time, one dimension is frequency, and the third dimension is amplitude.
Not only can we use this data to resynthesize a sound, but in doing so, we can treat time and frequency separately. That is we can slow a sound down without making the pitch go lower. Likewise, we could raise the pitch of a sound without making the sound wave shorter.
Back to Constant Gardener. This patch uses knob 1 to control the speed (or time element) of the re-synthesis. Knob 2 controls the pitch of the resynthesis. The third knob controls the balance between the dry audio input to the Organelle with the processed (resynthesized) sound. The final knob controls how much reverb is added to the sound. The aux button (or foot pedal) is used to turn the phase vocoder resynthesis on or off.
The phase vocoder part of the algorithm is sufficiently difficult such that I won’t attempt to go through it here, rather I will go through the reverb portion of the patch. As stated previously, knob four controls the balance between the dry (non-reverberated) and the reverberated sound. Thus value is then sent to the screen as a percentage, and is also sent to the variable reverb-amt using a number from 0 to 1 inclusive.
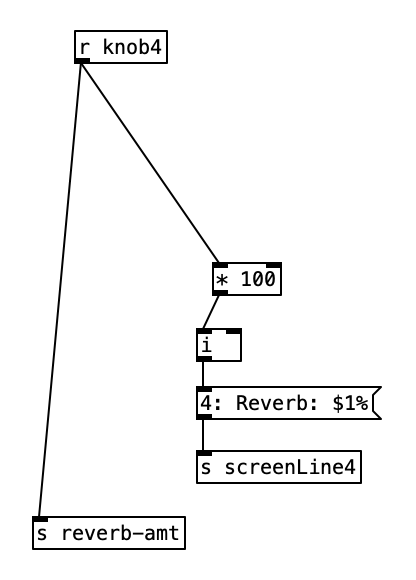
When the value of reverb-amt is recieved, it is sent to a subroutine called cg-dw. I’m not sure why the author of the patch used that name (perhaps cg stands for constant gardener), but this subroutine basically splits the signal in two, and modifies the value the will be returned out of the left outlet to be the inverse of the value of the right outlet (that is 1 – the reverb amount). Both values are passed through a low pass filter with cutoff frequency of 5 Hz, presumably to smooth out the signal.
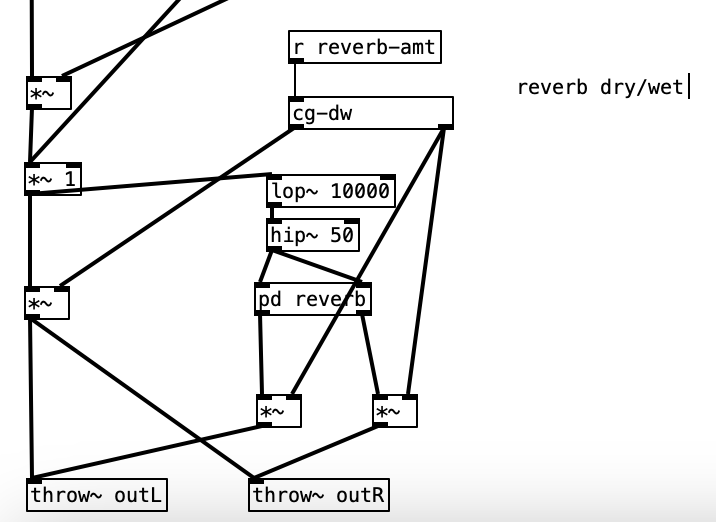
The object lop~ 10000 receives its input from a chain that can be traced back to the input of the dry audio coming from the Organelle’s audio input. This object is a low pass filter, which means that the frequencies below the cutoff frequency, in this case 10,000 Hz, to pass through the filter, which in return attenuates the frequencies above the cutoff frequency. More specifically, lop is a one-pole, which means that the amount of attenuation is 6 dB per octave. A reduction of 6 dB effectively is half the power of the original. Thus, if the cutoff frequency of a low pass filter is set to 100 Hz, the power at 200 Hz (doubling a frequency raises the pitch an octave) is half of what it would normally be, and at 400 Hz, the power would be a quarter of what it would normally be.
In analog synthesis a two pole (12 dB / octave reduction) or a four pole (24 dB / octave) filter would be considered more desirable. Thus, a one pole filter can be thought of as a fairly gentle filter. This low pass filter is put in the signal chain to reduce the high frequency content to avoid aliasing. Aliasing is the creation of artifacts when a signal is not sampled frequently enough to faithfully represent a signal. Human beings can hear up to 20,000 Hz, but audio demands at least one positive value and one negative value to represent a sound wave. Thus, CD quality sound uses 44,100 samples per second. The Nyquist frequency, the frequency at which aliasing starts is half the sample rate. In the case of CD quality audio, that would be 22,050 Hz. Thus, our low pass filter reduces these frequencies by more than half.
The signal is then passed to the object hip~ 50. This object is a one-pole high pass filter. This type of filter attenuates the frequencies below the cutoff frequency (in this case 50 Hz). Human hearing goes down to about 20 Hz. Thus, the energy at this frequency would be attenuated by more than half. This filter is inserted into the chain to reduce thumps and low frequency noise.
Finally we get to the reverb subroutine itself. The object that does most of the heavy lifting in this subroutine is rev~ 100 89 3000 20. This is a stereo input, four output reverb unit. Accordingly the first two inlets would be the left and right input. The other four inlets are covered by creation arguments (100 89 3000 20). These four values correspond to: output value, liveness, crossover frequency, and high frequency dampening. The output value is expressed in decibels. When expressed in this manner we can think of a change of 10 dB as doubling or halving the volume of a sound. We often consider the threshold of pain (audio so loud that it is physically painful to us) as starting around 120 dB. Thus, 100 dB, while considered to be loud, is 1/4 as loud as the threshold of pain. The liveness setting is really a feedback level (how much of the reverberated sound is fed back through the algorithm). A setting of 100 would yield reverb that would go on forever, while the setting 80 would give us short reverb. Accordingly, 89 gives us a moderate amount of reverb.
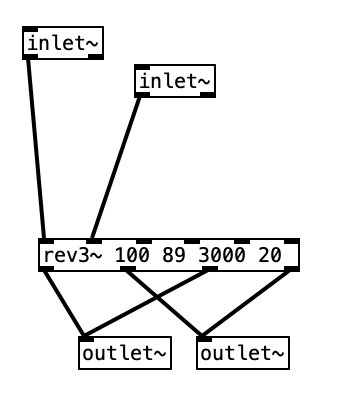
The last two values, cross over frequency and high frequency dampening work somewhat like a low pass filter. In the acoustic world low frequencies reverberate very effectively, while high frequencies tend to be absorbed by the environment. That is why a highly reverberant space like a cave or a cathedral has a dark sound to its reverb. In order to model this phenomenon, most reverb algorithms have an ability to attenuate high frequencies built into them. In this case 3,000 Hz is the frequency at which dampening begins. Here dampening is expressed as a percentage. Thus, a dampening of 0 would mean no dampening occurs, while 100 would mean that all of the frequencies about the crossover frequency are dampened. Accordingly, 20 seems like a moderate value. The outlets from pd reverb are then multiplied by the right outlet of cg-dw, applying the amount of reverb desired, and sent to the right and left outputs using throw~ outL and throw~ outR respectively.
For the EYESY I used the patch Mirror Grid Inverse – Trails. The EYESY’s five knobs are used to control: line width, line spacing, trails fade, foreground color, and background color. EYESY programming is accomplished in the language Python, and utilizes subroutines included in a library designed for creating video games called pygame.
An EYESY program is typically in four parts. The first part is where Python libraries are imported (pygame must be imported in any EYESY program). This particular program imports: os, pygame, math, and time. The second part is a setup function. This program uses the code def setup(screen, etc): pass to accomplish this. The third part is a draw function, which will be executed once for every frame of video. Accordingly, while this is where most of the magic happens, it should be written to be as lean as possible in order to run smoothly. Finally, the output should be routed to the screen.
In terms of the performance, I occasionally used knob 2 to change the pitch. I left reverb at 100%, and mix around 50% for the duration of the improvisation. I could have used the keyboard of the Organelle to play specific pitched versions of the audio input. Next month I hope to tackle additive synthesis, and perhaps use a webcam with the EYESY. Given that I’ve given a basic explanation of the first two parts of an EYESY program, in future months I hope to go through EYESY programs in greater detail.
