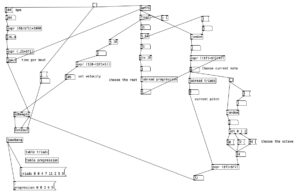
In the previous post, we had an introduction to patches in Pure Data using a patch that plays a scale in quarter, eighth, and sixteenth notes in three different octaves. In this post we’ll be looking a way to generate diatonic triads using a chord progression. Again, these patches are intended to teach concepts of music theory along with concepts of music technology.
Some portions of this patch are similar to portions of the previous patch, so we’ll give them only a brief mention. For instance, the portion (in the upper left) that translates tempo (in this case 104 beats per minute) into time per beat (expressed in milliseconds) is essentially the same. Here is multiplied by .25 to yield a constant sixteenth note rhythm. Likewise, the portion of the patch that actually makes the notes and outputs them to MIDI (middle left) is essentially the same.
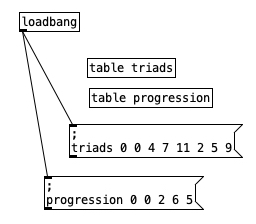
We have previously introduced loadbang and tables. Here we use tables to define diatonic triads in C Major. Using C as zero, triads 0 0 4 7 11 2 5 9 presents the notes of C major in stacked thirds (C, E, G, B, D, F, A respectively). If we pull out three consecutive numbers from this table, we will get a root, third, and fifth of a triad. We can wrap the table around to the beginning using modular mathematics (in this case mod seven) to yield thirds and fifths of the A chord, as well as the fifth of the F chord.
We can define a diatonic chord progression by noting the table position of the root of the chord in the triads table. Accordingly progression 0 0 2 6 5 gives us the roots C, G, A, and F. Given the layout of Major and minor thirds within a Major scale, this gives us the specific harmonies, C Major, G Major, A minor, and F Major. Fans of popular music will recognize this progression from numerous songs, including “Don’t Stop Believing,” “Can You Feel the Love Tonight,” and “Country Roads.”
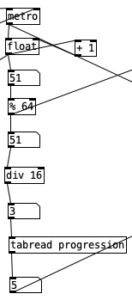
The metronome used in the patch ticks off sixteenth note increments, so the % 64 object beneath the counter reduces the counter to a four measure sequence (four groups of 16 sixteenth notes adds up to 64 notes). This number is used in the object div 16, which yields the whole number portion (non-fractional portion) of the number being divided by 16. This will result in the values 0, 1, 2, or 3. This is essentially the current measure number in terms of the direction. Feeding this to tabread progression. Will give the index value for the root of that measure’s chord when used with the triads table.
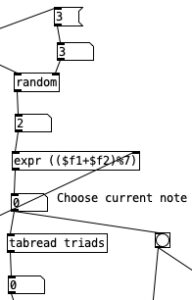
The value from the tabread progression object is sent to the right inlet of the expr statement in the segment above. A random number between 0 and 2 inclusive is fed to the left inlet of the same expr statement. The random number represents whether the note created will be a root (0), a third (1), or a fifth (2). by adding these two values together we get the index of the specific pitch the triads table. Using mod 7, % 7 in the expr statement, insures that if we go beyond the end of the the triads table that we will wrap around the beginning of the table. This index is then passed to tabread triads, which returns the numeric value of the specified note.
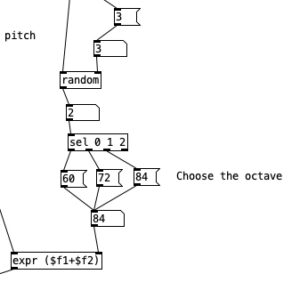
Note that in the previous segment a second outlet from the number object beneath the expr statement is then sent to a bang. This activates the random code in the segment above, namely the selection of a random number between 0 and 2 inclusive. This number is passed to a sel statement, specifically, sel 0 1 2. This object activates one of the three leftmost outlets, depending upon whether it is passed a 0, 1, or 2 (respectively left to right). the rightmost outlet activates if anything besides 0, 1, or 2 is encountered. In this case we pass the three left most outlets to three messages, 60, 72, and 84. These numbers are three different octaves of C (middle C, C5, and C6 respectively). Those messages are fed to a number object, which in turn is fed to the right inlet of an expr statement. The left inlet of this expr statement comes from the output of tabread triads. Thus, in expr ($f1+$f2) the pitch is added to one of three octaves, yielding a random arpeggiation across three octaves of pitch space. Let’s listen to the results of this patch below.