Tag: Pure Data

Posted on

Experiment 5: 2opFM

As was the case with Experiment 4, this month’s experiment has been a big step forward, even if the music may not seem to indicate an advance. This is due to the fact that this is the first significant Organelle patch that I’ve created, and that I’ve figured out how to connect the EYESY to wifi, allowing me to transfer files to and from the unit. The patch I created, 2opFM, is based upon Node FM by m.wisniowski.

As the name of the patch suggests it is a two operator FM synthesizer. For those who are unfamiliar with FM synthesis, one of the two operators is a carrier, which is an audible oscillator. The other operator is an oscillator that modulates the carrier. In its simplest form, we can think of FM synthesis as being like vibrato. One oscillator makes sound, while the other oscillator changes the pitch of the carrier. We can think of two basic controls that affect the nature of the vibrato, the speed (frequency) of the modulating oscillator, and the depth of modulation, that is how far away from the fundamental frequency does the pitch move.

What makes FM synthesis different from basic vibrato is that typically the modulating oscillator is operating at a frequency within the audio range, often at a frequency that is higher in pitch than that of the carrier. Thus, when operating at such a high frequency, the modulator doesn’t change the pitch of the carrier. Rather it functions to shape the waveform of the carrier. FM Synthesis is most often accomplished using sine waves. Accordingly, as one applies modulation we start to add harmonics, yielding more complex timbres.

Going into detail about how FM synthesis shapes waveforms is well beyond the scope of this entry. However, it is worth noting that my application of FM synthesis here is very rudimentary. The four parameters controlled by the Organelle’s knobs are: transposition level, FM Ratio, release, and FM Mod index. Transposition is in semitones, allowing the user to transpose the instrument up to two octaves in either direction (up or down). FM Ratio only allows for integer values between 1 and 32. The fact that only integers are used here means that the result harmonic spectra will all conform to the harmonic series. Release refers to how long it will take a note to go from its operating volume to 0 after a note ends. The FM Mod index is how much modulation is applied to the carrier, with a higher index resulting in more harmonics added to a given waveform. I put this parameter on the leftmost knob, so that when I control the organelle via my wind controller, a WARBL, increases in air pressure will result in richer waveforms.

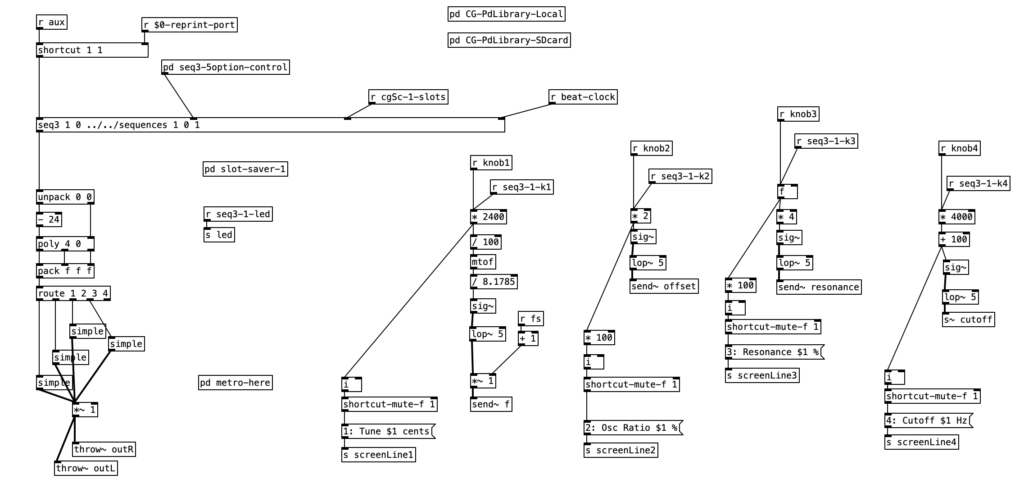
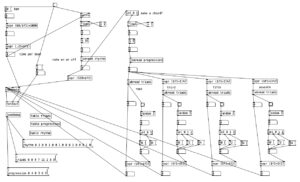
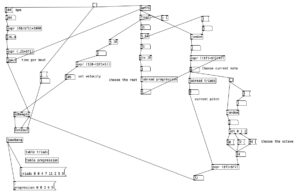
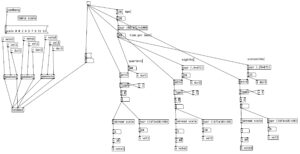
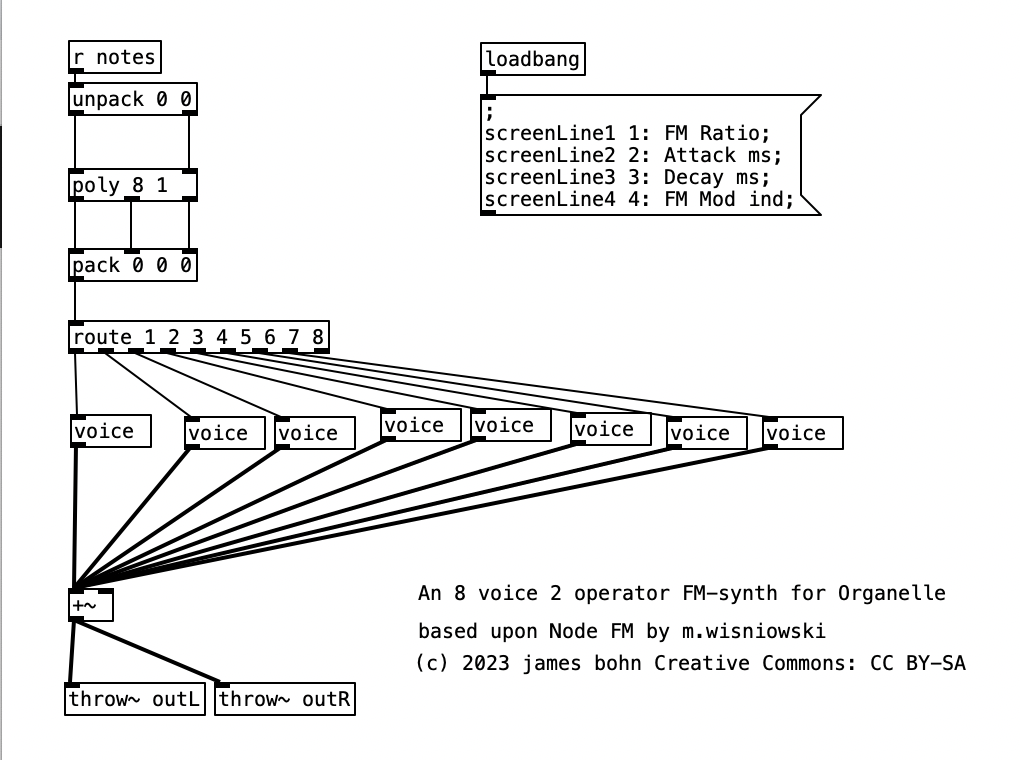
As can be seen in the screenshot of main.pd above, 2opFM is an eight voice synthesizer. Eight voice means that eight different notes can be played simultaneously when using a keyboard instrument. Each individual note is passed to the subroutine voice. Determining the frequency of the modulator involves three different parameters: the MIDI note number of the incoming pitch, the transposition level, and the FM ratio. We see the MIDI note number coming out of the left outlet of upack 0 0 on the right hand side, just below r notesIN-$0. For the carrier, we simply add this number to the transposition level, and then convert it to a frequency by using the object mtof, which stands for MIDI to frequency. This value is then, eventually passed to the carrier oscilator. For the modulator, we have to add the MIDI note number to the transposition level, convert it to a frequency, again using mtof, and multiplying this value by the FM Ratio.

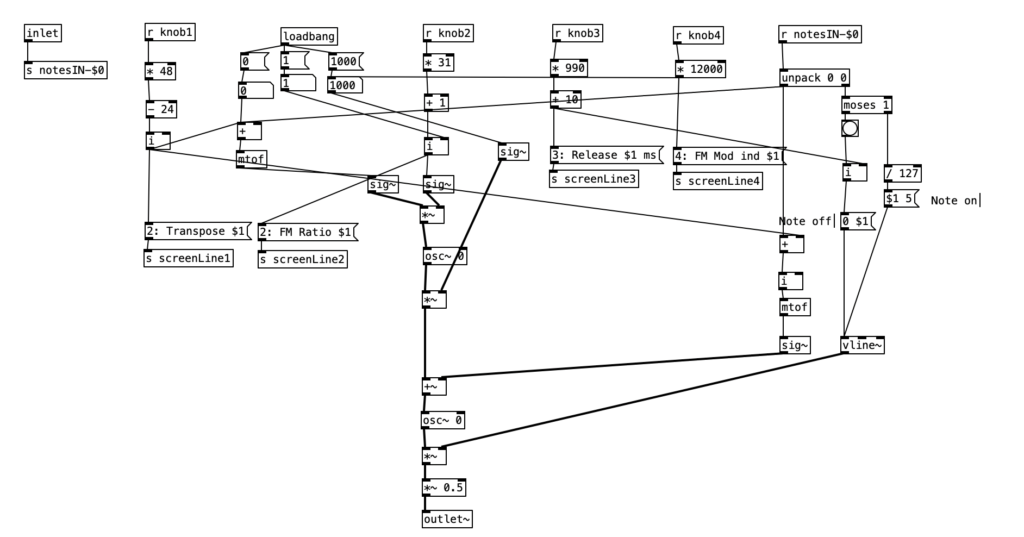
In order to understand the flow of this algorithm, we first have to understand the difference between control signals and audio signals. Audio signals are exactly what they sound like. In order to have high quality sound audio signals are calculated at the sample rate, which is 44,100 samples per section by default. In Pure Data, calculations that happen at this rate are indicated by a tilde following the object name. In order to save on processor time, calculations that don’t have to happen so quickly are control signals, which are denoted by a lack of a tilde after the object name. These calculations typically happen once every 64 samples, so approximately 689 times per second.

Knowing the difference between audio signals and control signals, we can now introduce two other objects. The object sig~ converts a control signal into an audio signal. Likewise, i converts a float (decimal value) to an integer, by truncating the value towards zero, that is positive values are rounded down, while negative values are rounded up.

Keep in mind the loadbang portion of voice.pd is used to initialize the values. Here we see the transposition level set at zero, the FM ratio set to one, and the FM Mod index set to 1000. The values from the knobs come in as floats between 0 and 1 inclusive. Thus, typically in order to get useable values we have to perform mathematical operations to rescale them. Under knob 1, we see the transposition level multiplied by 48, and then we subtract 24 from that value. This will yield a value between -24 (two octaves down) and +24 (two octaves up). Under knob 2, we see the FM ratio multiplied by 31, and then we add one to this value, resulting in a value between 1 and 32 inclusive. Both of these values are converted to integers using i.

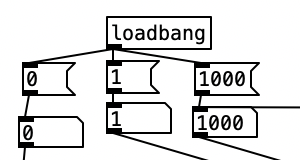
The scaled value of knob 1 (transposition level) is then added to the MIDI note number, and then turned into a frequency using mtof and converted to an audio signal using sig~. This is now the fundamental frequency of carrier oscillator. In order to get the frequency of the modulator, we need to multiply this value to the scaled value of knob 2. This frequency is then fed to the leftmost inlet of the modulating oscillator (osc~). The output of the modulating oscillator is then multiplied by the scaled output of knob 4 (0 to 12,000 inclusive), which is then in turn multiplied by the fundamental frequency of the carrier oscillator before being fed to the leftmost inlet of the carrier oscillator (osc~). While there is more going on in this subroutine, this explains how the core elements of FM synthesis are accomplished in this algorithm.

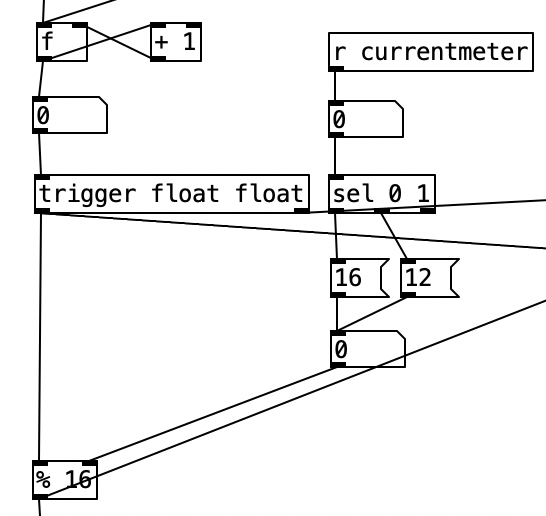
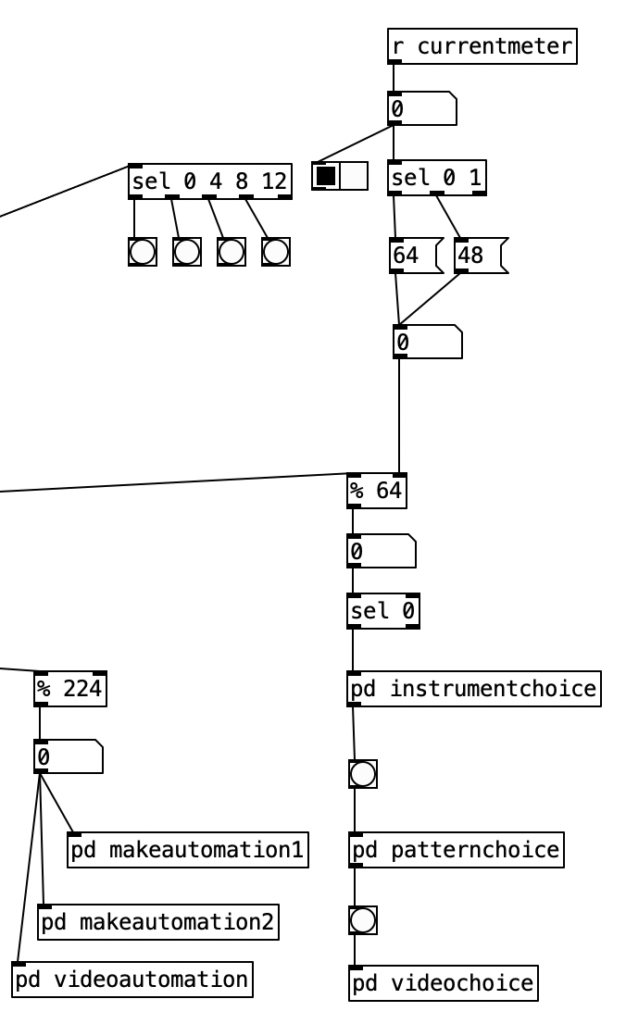
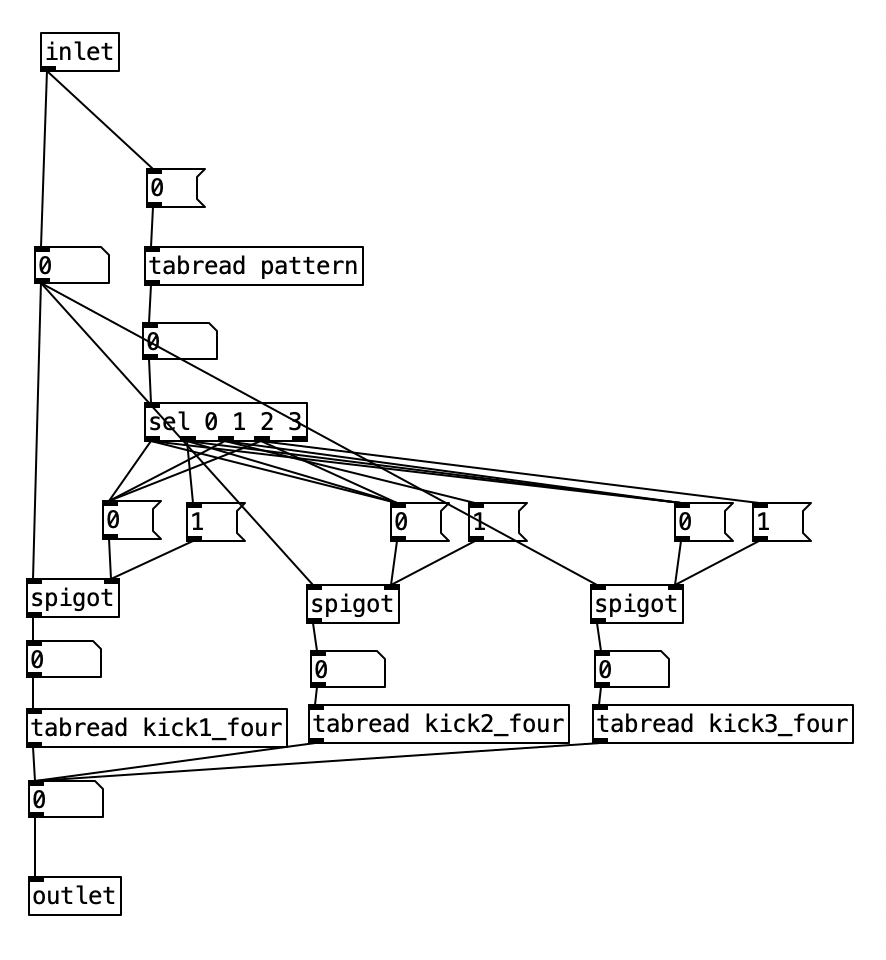
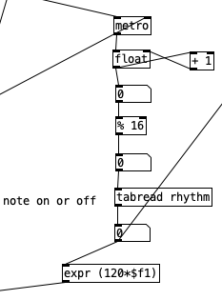
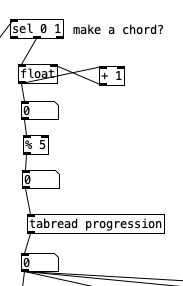
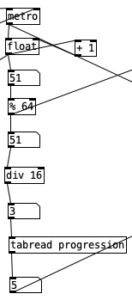
The algorithm that is used to generate the accompaniment is largely the same as the one used for Experiment 4 with a couple of changes. First, after completing Experiment 4 I realized I had to find a way to set the sixteenth note counter to zero every time the meter is changed. Otherwise, occasionally when changing from one meter to another there may be one or two extra beats. However, reseting the counter to zero ruins the subroutine that sends automation values. Thus, I had to use two counters, one that keeps counting without being reset (on the right) and one that gets reset every time the meter changes (on the left).

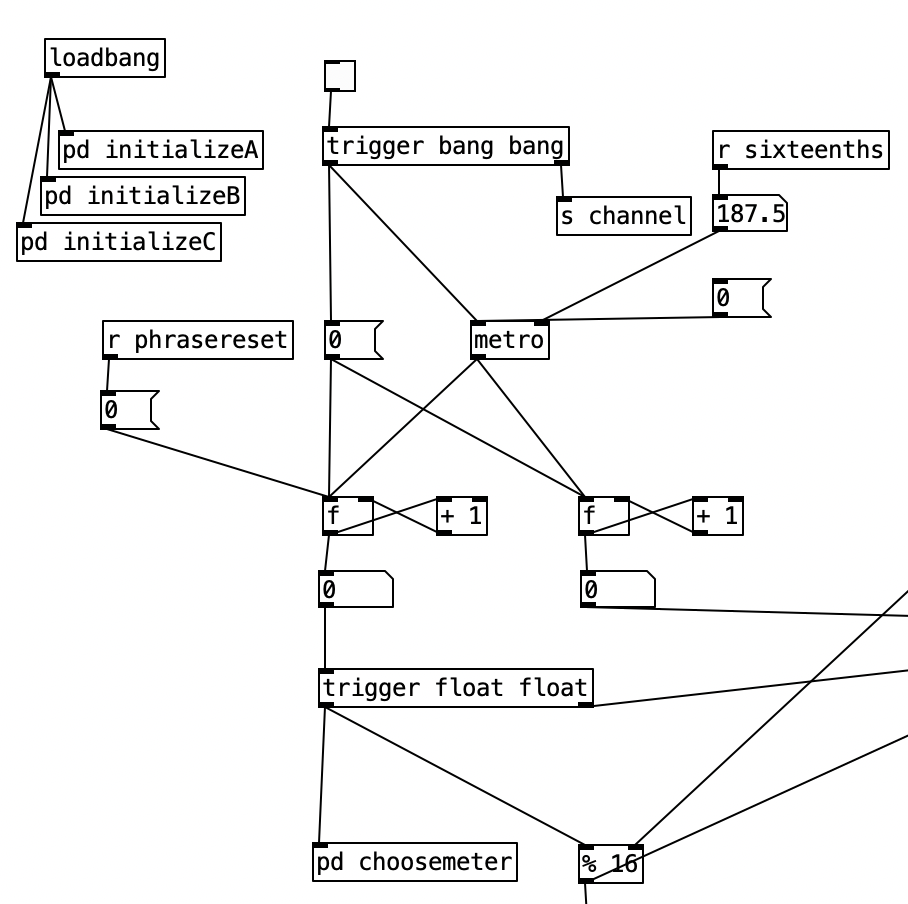
Initially I made a mistake by choosing the new meter at the beginning of a phrase. This caused a problem called a stack overflow. At the beginning of a phrase you’d chose a new meter, which would cause the phrase to reset, which would a new meter to be chosen, which then repeats in an endless loop. Thus, I had chose a new meter at the end of a phrase.

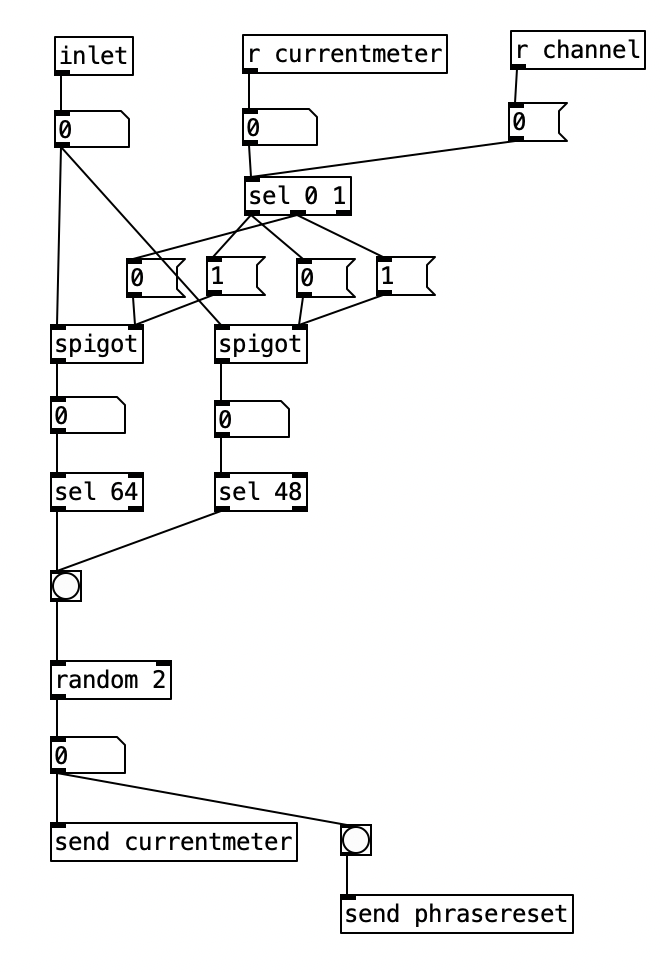
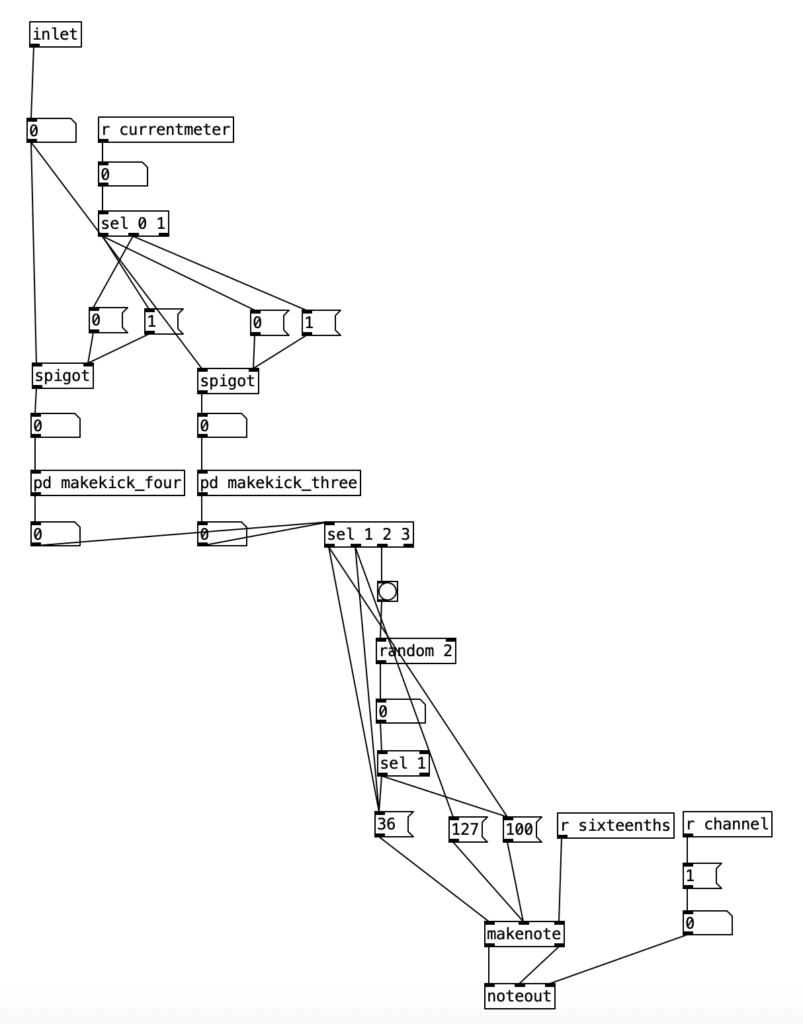
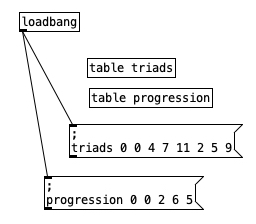
Inside pd choosemeter, we see the phrase counter being sent to two spigots. This spigots are turned on or off from depending on the value of currentmeter. The value 0 under r channel sets the meter for the first phrase to 4/4. Using the nomenclature of r channel is a bit confusing, as s channel is included in loadbang, and was simply included to initialize the MIDI channel numbers for the algorithm. In a future iteration of this program, I may retitle these values as s initializevalues and r initializevalues to make more sense.

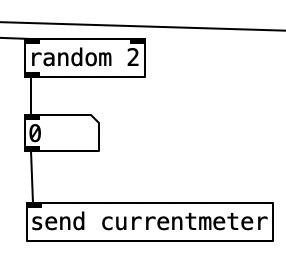
Underneath the two spigots, we see sel 64 and sel 48, This finds the end of the phrase when we are in 4/4 (64) or 3/4 (48). Originally I had used the values 63 and 47 as these would be the numbers of the last sixteenth note of each phrase. However, when I did that I found that the algorithm skipped the last sixteenth note of the phrase. Thus, by using 64 and 48 I actually am choosing the meter at the start of a phrase, but now reseting the counter to zero no longer triggers a recursive loop. Regardless, whenever either sel statement is triggered the next meter is chosen randomly, with zero corresponding to 4/4 and 1 corresponding to 3/4. This value is then sent to other parts of the algorithm using send currentmeter, and the phrase is reset by sending a bang to send phrasereset.

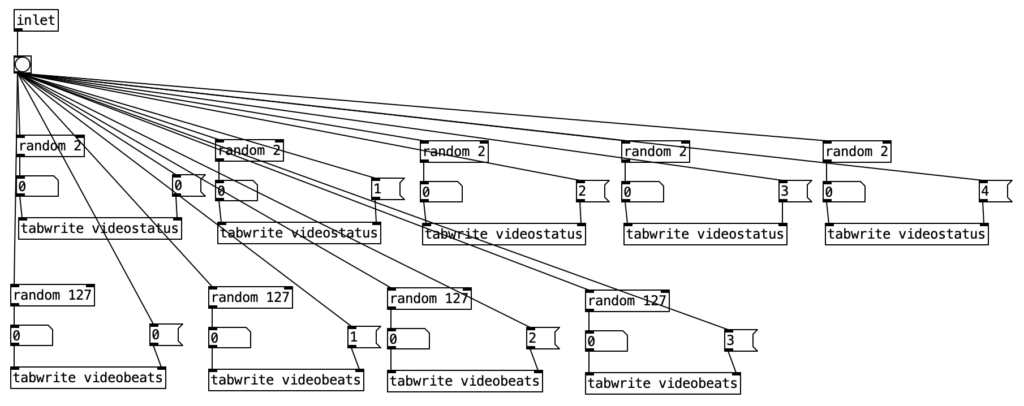
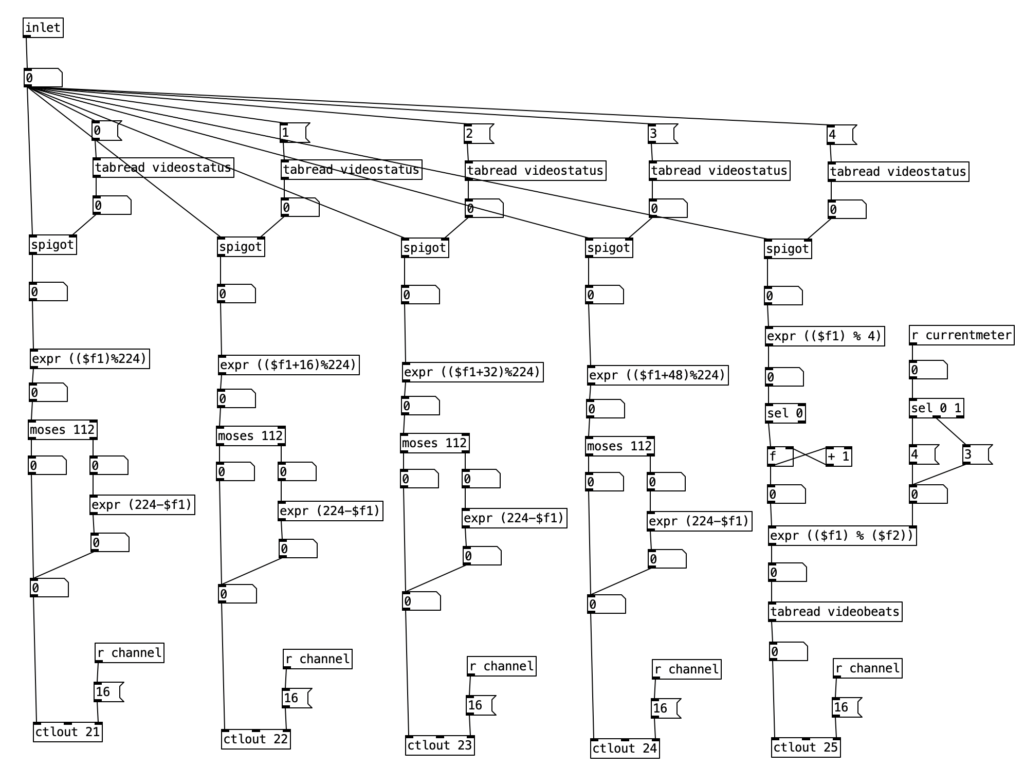
As previously noted, I figured out how to connect the EYESY to wifi, allowing me to transfer files two and from the unit. Amongst other things, this allows me to download new EYESY programs from patchstorage.com and add them to my EYESY. I downloaded a patch called Image Shadow Grid, which was developed by dudethedev. This algorithm randomly grabs images stored inside a directory, adds them to the screen, and manipulates them in the process.

I was able to customize this program without changing any of the code simply by changing out the images in the directory. I added images related to a live performance of a piece from my forthcoming album (as Darth Presley). However, up to this point I’d been using the EYESY to respond mainly to audio volume. Some algorithms, such as Image Shadow Grid, use triggers to incite changes in the video output. The EYESY has several trigger modes. I chose to use the MIDI note trigger mode. However, in order to trigger the unit I now have to send MIDI notes to the EYESY.

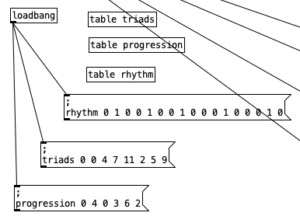
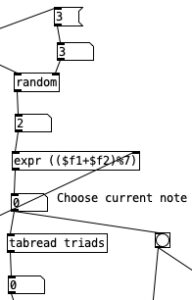
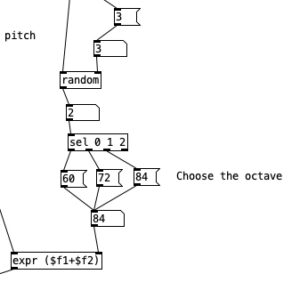
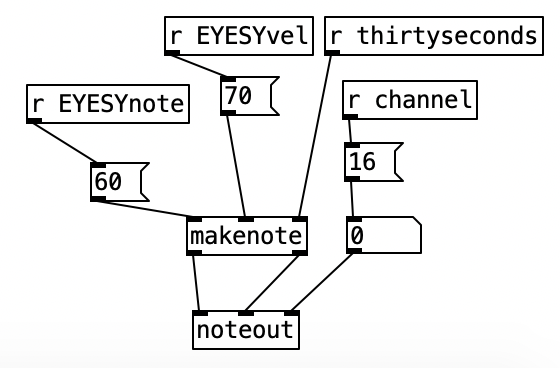
This constitute the other significant change to the algorithm that generates the accompaniment. I added a subroutine that sends notes to the EYESY. Since the pitch of the notes don’t matter, I simply send the number for middle C (60) to the unit. Otherwise the subroutine which determines whether a note should be sent to the EYESY functions just like those used to generate any rhythm, that is it selects between one of three rhythmic patterns for each of the two meters, each pattern of which is stored as an array.

As with last month, the significant weakness in this month’s experiment is my lack of practice on the WARBL. Likewise, it would have been useful if I had the opportunity to add a third meter to the algorithm that generates the accompaniment. The Organelle program 2opFM is not quite as expressive with the WARBL as it had been in experiment 2 and 4. Changes in the FM Mod Index aren’t as smooth as I had hoped they’d be. Perhaps if I were to expand the patch further, I’d want to add a third operator, and separate the FM Mod Index into two parts, one where you set the maximum level of the index, and another where you set the current level, so you can set it where the maximum breath pressure on the WARBL only yields a subtle amount of modulation.

In terms of the EYESY, I doubt I will begin writing programs for it next month, I may experiment with already existing algorithms that allow the EYESY to use a webcam. However, hopefully by October I can be hacking some Python code for the EYESY. My current plan is to experiment with some additive synthesis next month, so stay tuned.

Posted on

Experiment 4: NES EWI

While this month’s experiment may not seem musically much more advanced than Experiment 2, this month has actually been a significant step forward for me. I finished reading Organelle: How to Program Patches in Pure Data by Maurizio Di Berardino. More importantly, I finally got the WiFi working on my Organelle which allows me to transfer patches back and fourth between my laptop and the Organelle. I used that feature to transfer a patch called NESWave Synth by a user called blavatsky. This patch uses waveforms from the Nintendo Entertainment System, the Commodore 64, and others as a basis for a synthesizer. However, the synthesizer allows one to mix in some granular synthesis, add delay, add a a phasor, and other fancy features.

I made one minor tweak to NESWave Synth. In experiment 2 I used my WARBL wind controller to control the filter of Analog Style, I wanted to do the same with NESWave. On Analog Style, the resonance of the filter is on knob 3 and the cutoff frequency is on knob 4. On NESWave Synth, these to settings are reversed. So, I edited NESWave Synth so resonance is on knob 3 and cutoff frequency is on knob 4. I titled this new version of the patch NES EWI. This patch me to go from controlling Analog Style to NES EWI without changing the settings on my WARBL.

As NESWave Synth / NES EWI has a lot of other features / settings. During this experiment, I setup all the parameters of the synth the way I wanted, and didn’t make any changes in the patch as I performed, although again the breath pressure of the WARBL was controlling the filter cutoff frequency. Another user noted that NESWave Synth is complicated enough to warrant patch storage, although to the best of my knowledge no one has implemented such a feature yet.

The tweak I made to NESWave Synth is insignificant enough to not warrant coverage here. Accordingly I’ll go over changes I made to the PureData algorithm that generated the accompaniment for Experiment 2. Experiment 2 uses the meter 4/4 exclusively. I’ve been wanting to build an algorithm that randomly selects a musical meter at the beginning of each phrase. While the basic mechanics of this is easy, in order to add a second meter, I have to double the number of arrays that define the musical patterns.

In Experiment 4 I add the possibility of 3/4. Choosing between the two meters is simple. Inside the subroutine pd instrumentchoice I added a simple bit of code that randomly chooses between 0 and 1, and then sends that value out as currentmeter.

However, making this change causes three problems. The first is that the length of each measure now has change from 16 sixteenth notes to 12 sixteenth notes. That problem is solved in the main routine by adding an object that receives the value of currentmeter and uses that to select between an option that passes the number 16 or the number 12 to the right inlet of a mod operation on the global sixteenth note counter. This value will overwrite the initial value of 16 in the object % 16. As I write this, I realize I need to also reset the counter to 0 whenever I send a new meter so every phrase starts on beat 1. I can make that change in the next iteration of the algorithm.

The next problem is that I had to change the length of each phrase from 64 (4 x 16) for 4/4 to 48 (4 x 12) for 3/4. This is solved exactly the same way by passing the value of currentmeter to an object that selects either 64 or 48, and passes that value to the right inlet of a mod operation, overwriting the initial value of 64. Note that I also pass the value of currentmeter to a horizontal radio button so I can see what the current meter is. I can’t say that I actually used this in performance, but as I practice with this algorithm I should be able to get better at changing on the fly between a 4/4 feel and a 3/4 feel. Also, this should be much easier for me when I play an instrument I am more comfortable with than the EWI. I have also added a visual metronome using sel 0 4 8 12 each of which passes to a separate bang object. Doing this will cause each bang to flash on each successive beat. In future instances of this algorithm I may choose to just have it show where beat one is, as counting beats will become more complicated as I add asymetrical meters.

The final problem is that every subroutine that generates notes (pd makekick, pd makesnare, pd makeclap, pd makehh, pd makecymbal pd maketoms pd makecowbell pd makepizz, pd makekeys, pd makefm) needs to be able to switch between using patterns for 4/4 and patterns for 3/4. While I made these changes to all 10 subroutines, it is the same process for each, so I’ll only show one version. Let’s investigate the pd makekick subroutine. The object inlet receives the counter for the current sixteenth note, modded to 16 or 12. This value is then passed to the left inlet of two different spigot objects. In PureData spigots pass the value of the left inlet to the outlet if the value at the right inlet is greater than zero. Thus, we can take the value of currentmeter to select which spigot gets turned on, and conversely, which one gets turned off, using the 0 and 1 message boxes.

Now we know which meter is active, we will then pass to one of two subroutines which picks the current pattern. One of these subroutines pd makekick_four is for 4/4. The other, pd makekick_three is for 3/4. Both have essentially the same structure, so let’s look inside pd makekick_four. This subroutine uses the same structure as pd makekick. Again, the inlet receives the current value of the sixteenth note counter. Again, we use spigots to route this value, however, this time we use three spigots as there are three different patterns that are possible. This routing is accomplished using the current value of pattern. The 0 position of this array stores the value for kick drum patterns. Technically speaking, there are four different patterns, 0, 1, 2, 3, with the value 0 meaning that there is no active pattern, resulting in no kick drum pattern. Again, a sel statement that passes to a series of 0 and 1 message boxes turn on and off the three spigots. The object tabread objects below read from three different patterns kick1_four, kick2_four, kick3_four. The value at this point is passed back out to the pd makekick subroutine. Since the possible values, 0, 1, 2, or 3, are the same whether the pattern is in 4/4 or 3/4, these values are then passed to the rest of the subroutine, which either makes an accented note, an unaccented, note, or calculates a 50% chance of an unaccented occuring. A fourth possibility, no note, happens when the value is 0. By not including 0 in the object sel 1 2 3 we insure no note will happen in that case.

While I still haven’t looked into programming the EYESY, I did revise the PureData algorithm that controls the EYESY. In Experiment 2, all of the changes to the EYESY occur very gradually, resulting in slowly evolving imagery. In Experiment 4, I wanted to add some abrupt changes that occur on the beat. Most EYESY algorithms use knob 5 to control the background color. I figure that would be most apparent change possible, so in the subroutine pd videochoice I added code that would randomly choose four different colors (one for each potential beat), and to store them in an array called videobeats. Notice that each color is defined as a value between 0 and 126 (I realized while writing this, I could have used random 128) as we use MIDI to control the EYESY, and MIDI parameters have 128 different values.

Now we have revise pd videoautomation to allow for this parameter control. The first four knobs use the same process that we used in Experiment 2. For the fifth knob, the 4 position in the array videostatus, we first check to see whether changes should happen for that parameter by passing the output of tabread videostatus to a spigot. When tabread videostatus returns a one, the spigot will turn on, otherwise, it will shut down. When the spigot is open, the current value of sixteenth note counter is passed to an object that mods the by 4. When this value is 0, we are on a beat. We then have a counter that keeps track of what the current beat number is. We then however, have to mod that either 4 for 4/4 or 3 for 3/4. The is accomplished using expr (($f1) % ($f2)). Here we pass the current meter to the right inlet, corresponding to $f2. We do thus using the value of currentmeter to select between a 4 and 3 message box. We can then get the color corresponding to the beat by returning the value of videobeats, and send that out to the EYESY using ctrlout 25 (25 being the controller number for the fifth knob of the EYESY).

In terms of the video, it is clear that I really need to practice my EVI fingerings. I am considering forcing the issue by booking a gig on the instrument to force me to practice more. I find that the filter control on Analog Style felt more expressive to me than the control on NES EWI. Though perhaps I need to recalibrate the breath control on the WARBL. I hope to do a more substantial hack next month, perhaps creating a two operator FM instrument. I also hope to connect the EYESY to WiFi so I can add more programs to it.

Posted on

Experiment 3: Deterior

June has been busy for me. I’m behind where I wanted to be at this point in my research. This is due in part to not having a USB WiFi adapter to transfer files onto the Organelle and the EYESY. Accordingly, this month’s post will be light on programming, focusing on the Pure Data object route. I’ll be ordering one later this week, and will hopefully be able to take a significant step forward in July.

Accordingly, my third experiment in my project funded by Digital Innovation Lab at Stonehill College investigates the use of the preset patch Deterior (designed by Critter and Guitari). Deterior is an audio looper combined with audio effects in a feedback loop. In this experiment I run audio from a lap steel guitar.

The auxiliary key is used in conjunction with the black keys of the keyboard to select various functions. The lowest C# toggles loop recording on or off , the next D# stores the recording, the F# reverts to the most recent recording (removing any effects), the G# empties the loop, while A# toggles the input monitor. The upper five black keys of the instrument toggle on or off the five different effects that are available: noise (C#), clip (D#), silence (F#), pitch shift (G#), and filter (A#). The parameters of these effects cannot be changed from the Organelle, they can only be turned on or off. The routing of these auxiliary keys is accomplished through the subroutine shortcut.pd, using the statement route 61 63 66 68 70 73 75 78 80 82. Note that these numbers correspond to the MIDI note numbers for the black keys from C#4 to A#5.

A similar technique is used with the white keys of the instrument. These keys are used as storage slots for recorded loops, which can be recalled at any time once they are stored. This is initiated in pd slots, using route 60 62 64 65 67 69 71 72 74 76 77 79 81 83. These numbers correspond to the white keys from C4 to B5.

In this experiment I start using only filtering. Eventually I added silence, clipping, noise, and finally pitch shifting. Specifically, you can hear noise entering at 5:09. After adding all the effects in I stopped playing new audio, and instead focused on performing the knobs of the Organelle. Near the end of the experiment I start looping and layering a chord progression: Am, Dm, C#m, to Bm. When I introduce this progression I add one chord from this progression at a time.

In terms of the EYESY, I ran the recording through it so I would have my hands free to perform the settings. Again, I used a preset as I did not have a wireless USB connection to transfer files between my laptop and the EYESY. Hopefully next month I should be able to do deeper work with the EYESY.

Like Experiment 1, I had a lot of 60 cycle hum in the recording, which I tried to minimize by turning down the volume on the lap steel when I’m not recording sound. That process created it’s own distracting aspect of having the 60 cycle hum fade in and out in a repeating loop.

Posted on

Experiment 2: Analog Style


May has been a busy month for me. Thus, my second experiment in my project funded by Digital Innovation Lab at Stonehill College investigates the use of the preset patch Analog Style (designed by Critter and Guitari). To be specific, I am using a WARBL wind controller with EVI fingering to control the patch. I am using the breath control on the WARBL to control the cutoff frequency of Analog Style (using MIDI controller 24).

Due to the busyness of the end of the semester, this experiment features no original programming on the organelle. However, I did create a program in Pure Data to create accompaniment and drive the EYESY. To accompany the experiment, I used the H.E.A.P, the Housatonic Electronic Algorithmic Philharmonic. This a fun, frivolous name I’ve given to a small, battery powered synthesizer / sampler setup I’ve assembled for live performance. It consists of three synthesizers / samplers: a Volca Sample 2 (which provides 10 channels of late 1980s style lo fidelity digital sampling), a Volca Keys (which can be used as an analog monophonic or 3 note polyphonic synthesizer), and a Volca FM 2 (which is a clone of the 1980s classic, the Yamaha DX7, the best selling synthesizer of all time). I’ve also begun to think of the EYESY, as we’ll see later, as part of the H.E.A.P.

I won’t go into great detail about the program that generates the accompaniment for Experiment 2, as I have other blog posts that go into detail about various algorithms included in the program. Ultimately, the program is intended to generate relatively generic, but fairly usable R&B esque slow jams. The music is in common time using sixteenth notes. The portion of the program including and beneath % 16 (mod 16) ensures that the resulting music will have 16 pulses per measure. Likewise, the instrumentation and musical patterns change every four measures. This is enabled by the part of the program including and beneath % 64 (four measures of sixteenth notes adds up to 64).

The Volca Sample is being used to provide the drum beat, and some string pizzicato (see pd makepizz). The Volca Keys provides some synthesized bass patterns that run two measure loops. The Volca FM provides four chord, four note chord progressions that repeat every two measures. To create these chord progressions I used some music programming techniques that I’ve covered in a previous blog entry, though in this experiment I am use the brass friendly key of G minor.

One of the newer programming tricks I used in this program is an algorithm designed to drive the EYESY. While the EYESY generates hypnotic, interactive video animations, left to its own devices it can get a bit repetitive fairly quickly. In order to generate anything that seems even remotely dynamic some one needs to perform the EYESY by rotating its five knobs. This is an impossibility for any performing musician, save for a vocalist. Thankfully, we can do the equivalent of turning the knobs on the EYESY through MIDI using controllers 21 through 25.

The algorithm I’ve created to drive the EYESY is designed to make slow, evolving changes. To control these changes I’ve created a table called videostatus. It consists of five positions that contain a one or a zero to denote whether changes should be make or not made to a given knob during the current four measure phrase.

The subroutine pd videochoice is triggered at the beginning of every four measure phrase. It generates five different random numbers that are either a zero or a one. These results are then stored in the table videostatus.

The subroutine pd videoautomation updates the knob positions on the EYESY once every sixteenth note. It is passed the current sixteenth note number modded by the number 224, which corresponds to 14 measures of sixteenth notes. The subroutine contains five nearly identical columns, each of which corresponds to each of the five knobs on the EYESY. First the algorithm checks the current states of each of the five positions of videostatus table. When that value is one, that allows the current sixteenth note number to pass through the spigot. This value is passed through an expr statement that displaces the sixteenth note number. The column corresponding to knob one is not displaced, but each subsequent column is displaced by one measure (16 sixteenths), which is then modded to stay between 0 and 224. The statement moses 112 is used to determine whether we should be counting up to 112, or counting down to 0. This is accomplished by having numbers that are greater than 112 to pass through expr (224-$f1), which causes the result to get small as the input value is increased. The result of this is then passed to one of the five controller values (21-25) on MIDI channel 16 (the channel I’ve set my EYESY to).

Since I went over the mother patch in the previous experiment, I’ll start with going over main.pd for the Analog Style patch. We can see that knob one controls the tuning of the patch, while knob two creates an offset frequency for a second oscillator. The third knob sets the resonance of the low pass filter, while the fourth knob (the one I am controlling using the WARBL) sets the cutoff frequency of filter. To learn more about what low pass filters are, check out my blog entry on Low Pass Filters in LogicPro. However, to summarize briefly in relationship to the WARBL, when the amount of breath coming through is low, that in turn sets the cutoff frequency to be low as well, resulting in less sound (and only low frequency sound) to come out of the Organelle.

We can also see that this patch allows for sequencing when the aux button is down. However we will not go through how sequencing works today. We will however go into simple, which is the subroutine that creates the sound. We can see two oscillators, blsaw, in this subroutine that generate sawtooth waves. For more information on subtractive synthesis waveforms (including sawtooth waves), check out my blog entry on Subtractive Synthesis Waveforms in Logic Pro. One of those two blsaw oscillators is modified by the offset of knob two. The mixture of these two oscillators is passed to a low pass filter, moog~. This object also receives a center frequency to its center inlet, and a resonance value to its right most inlet. The outlet of this object is then attenuated slightly, *~ .75, before being sent to the subroutine’s outlet.

Again, I’ve found that the accompaniment generated by experiment.pd to be generic, but also fairly usable. It should be relatively easy to change the tempo, phrase length, or any number of musical patterns to create music that is stylistically different. Also, I enjoy slow evolving nature of EYESY generated video. I feel that turning on and off changes to various combinations of the five knobs add a degree of subtlety that aid in the dynamic nature of the video.

I am disappointed in my performance on the WARBL. I am still getting used to the EVI fingering on the instrument, so there are some very sour notes from time to time. However, I am very pleased with the range of the WARBL, as well as the subtle breath control the instrument provides. The fingering makes jumping octaves and fifths very easy. In future experiments I hope to get into hacking existing Organelle patches. I also plan to come up with variants of the videoautomation algorithm to create more sudden, less subtle changes to the EYESY’s settings.

Posted on

Experiment 1: Granular Freezer

The first experiment in my project funded by Digital Innovation Lab at Stonehill College investigates the use of the preset patch Granular Freezer (designed by Critter and Guitari) to process audio . In this case the audio is coming from a lap steel guitar. In that I’m just getting used to both the Organelle and the EYESY, I will simply be improvising using a preset with the EYESY.

While describing his concept of stochastic music, composer Iannis Xenakis essentially also described the idea of granular synthesis in his book Formalized Music: Thought and Mathematics in Music . . .

“Other paths also led to the same stochastic crossroads . . . natural events such as the collision of hail or rain with hard surfaces, or the song of cicadas in a summer field. These sonic events are made out of thousands of isolated sounds; this multitude of sounds, seen as a totality, is a new sonic event. . . . Everyone has observed the sonic phenomena of a political crowd of dozens or hundreds of thousands of people. The human river shouts a slogan in a uniform rhythm. Then another slogan springs from the head of the demonstration; it spreads towards the tail, replacing the first. A wave of transition thus passes from the head to the tail. The clamor fills the city, and the inhibiting force of voice and rhythm reaches a climax. It is an event of great power and beauty in its ferocity. Then the impact between the demonstrators and the enemy occurs. The perfect rhythm of the last slogan breaks up in a huge cluster of chaotic shorts, which also spreads to the tail. Imagine, in addition, the reports of dozens of machine guns and the whistle of bullets adding their punctuations to this total disorder. The crowd is then rapidly dispersed, and after sonic and visual hell follows a detonating clam, full of despair, dust, and death.”

This passage by Xenakis goes into dark territory very quickly, but it is a scenario that harkened back to the composer’s past when he lost an eye during a conflict with occupying British tanks during the Greek Civil War.

Granular synthesis was theorized before it was possible. Its complexity requires computer technology that at the time it was theorized was not yet powerful enough. Granular synthesis takes an audio waveform, sample, or audio stream and chops it into grains and then resynthesizes the sound by combining them into clouds. The synthesist can often control aspects such as grain length, grain playback speed, cloud density, as well as others. Since the user can control playback speed of grains independently of the speed to which a sound travels through a group of grains, granular synthesis allows one to stretch or compress the timing of sound without affecting pitch, as well as being able to change the pitch of a sound without affecting the duration of a sound.

Granular Freezer is sort of a budget version of Mutable Instruments Clouds. I call it a budget version, as Clouds allows for the control of more than a half dozen parameters of the sound, while Granular Freezer gives the user control of four parameters, namely grain size, spread, cloud density, and wet / dry mix. These four parameters correspond to the four prominent knobs on the Organelle. Spread can be thought of as a window, that kind of functions like a delay time. In other words it is a window of past audio that the algorithm draws from to create grains. As you turn the spread down the sound starts to sound like an eccentric slap (short) delay. Wet / dry mix is a very standard parameter in audio processing. It is the ratio of processed sound to original sound that is sent to the output. The Aux button can be used to freeze the sound, that is hold the current spread in memory until the sound is unfroze. You may also use a pedal to trigger this function. One feature of the algorithm that I didn’t use was using the MIDI keyboard to transpose the audio.

Since this is my first experiment with the Organelle, I’m not going to go through the algorithm in great detail, but I will give it an overview. All patches for the Organelle use a patch called a mother patch. The mother patch should never be altered. This controls input to and output from the Organelle. Such values are passed to and from the mother patch in order to avoid input and output errors. You can download the mother patch so you can develop instruments on a computer without having access to an Organelle. This is also a good way to check for coding errors before you upload a patch to your Organelle.

If we double click on the subroutine pd MIDI, we can see, amongst other things how the Organelle translates incoming MIDI controller data (controller numbers 21, 22, 23, & 24) to knob data . .

When we double click on pd audioIO, we can see how the mother patch handles incoming audio (left) as well as outgoing audio (right) . . .

Any given Organelle patch typically consists of a main program (by convention, named main.pd), as well as a number of self contained subpatches called abstractions. In the case of Granular Freezer, in addition to the main program there are three abstrations: latch-notes.pd, grain.pd, and grainvoice.pd. Given the complexity of the program, I will only go over main.pd.

In the upper right hand quadrant we see the portion of the algorithm that handles input and output. It also controls the ability to freeze the audio (pd freezer). The objects catch~ grainoutL and catch~ grainoutR receive the granularly processed audio from grainvoice.pd. The object r wetdry receives data from knob 4, allowing the user to control the ratio of unprocessed sound to processed sound.

The lower half of main.pd sets the numerical range for each of the four knobs, sends the data to wherever it is needed (as was done with wetdry), and sets & sends the text to be displayed on the Organelle’s screen. This last item causes the function of each knob to be displayed along with its current status. In the message box at the bottom of the screen, we see a similar item related to the aux key screenLine5. The part of the program that updates the display for screenLine5 is in pd freezer.

In the improvisation I run a six string lap steel using C6 tuning through a volume pedal, and then into the Organelle. I also use a foot switch to trigger the freeze function on the patch. Musically, I spend the bulk of the time improvising over an E pedal provided by an eBow on the open low E string. A lot of the improvisation is devoted to arpeggiating Am, C#m, and Em chords on the upper three strings of the instrument. During the beginning of the improvisation the mix is at 80% (only 20% of the original sound). I quickly move to 100% mix. Near the end I move to sliding pitches with the eBow. During this portion of the improvisation I experiment with the spread, and there’s a portion where I move the spread close to its minimal amount, which yields that eccentric slap delay sound (starts around 8:28). As I move the spread towards its upper end, I can use it as a harmonizer, as the spread holds the previous pitch in its memory as I move onto a new harmonizing pitch. At the end (around 9:15) I move the grain size down to the bottom (1 millisecond), and then turn the cloud density down to the bottom to function as a fade out.

With the EYESY I simply improvised the video using the audio of the video recording I made. With the mode I was using the first two knobs seemed to control the horizontal and vertical configuration of the polygons. These controls allow you to position them in rows, or in a diamond lattice configuration. You can even use these controls to get the polygons to superimpose to an extent. The middle knob seems to increase the size of the polygons, making them overlap a considerable amount. The two knobs on the right control the colors for the polygons and the background respectively. I used these to start from a green on black configuration in honor of the Apple IIe computer.

The video below will allow you to watch the EYESY improvisation and the musical improvisation simultaneously . . .

As I mentioned earlier, I consider Granular Freezer to be a budget version of Clouds. I have the CalSynth clone of Clones, Monsoon, in a synthesizer rack I’m assembling. It is a wonderful, expressive instrument that creates wonderful sounds. While Granular Freezer is a more limited instrument, it is still capable of creating some wonderful sounds. There are already a couple variants of Granular Freezer posted on PatchStorage. As I get more familiar with programming for the Organelle, I should be able to create a version of the patch that allows for far greater control of parameters.

All in all, I feel this was a successful experiment. I should be able to reuse the audio for other musical projects. However, there was some room for improvement. There was a little bit of 60 cycle hum that was coming through the system. This was likely due to a cheap pickup in my lap steel. Likewise, it would be nice if I cleaned up my studio so it would make for a less cluttered YouTube video. As I mentioned earlier it would be good to add more parameters to the Granular Freezer patch. I used Zoom to capture the video created by the EYESY, and it added my name to the lower left hand corner of the screen. Next time I may try using QuickTime for video capture to avoid that issue. By the end of the summer I hope to develop some PureData algorithms to control the EYESY to perform the video in an automated fashion. See you all back here next month for the next installment.

Posted on

Pure Data: Seventh Chord Stingers

In the previous post we looked at a random arpeggiator that uses diatonic chord progressions. In this entry we will be using the same technique for creating diatonic chord progressions, but we will be applying it to create block seventh chords that repeat in a sequencer like fashion. Again we use the same code used in the scale sequencer to translate tempo from beats per minute to time per beat (expressed in milliseconds). As mentioned, we use the same table, ; triads 0 0 4 7 11 2 5 9,  from the previous post to denote the notes of C Major, arranged as stacked thirds.

As we did in the previous patch, we can make a list of index numbers that relate to the triads table, which can be used to define the roots of a chord progression. In this case we are using the table ; progression 0 4 0 3 6 2. This results in the progression Dm7, CMaj7, Bm7(b5), Am7, G7. The other new element of this patch involves introducing a rhythmic pattern. This is accomplished using the table  rhythm, where we use 1 to indicate a chord happening, and 0 to mean a rest happening. The table includes 16 numbers, indicating a single measure of sixteenth notes. The resulting rhythm starts out using syncopation where the first three chord jabs occur once every three sixteenth notes (or a dotted eighth note). The final two chords occur on the off beats of beats three and four, yielding a pleasantly funky rhythm.

We use the rhythm table table in a very simple manner. We mod the counter to 16, resulting in a sixteenth note rhythm that repeats every measure. We then read the rhythm table. Multiplying that number, which will be a zero or a one, by 120 gives us a velocity. A velocity of zero results in makenote not generating a note, while the chord stabs will be reasonably loud at 120.

The number from tabread rhythm is then also passed to a sel statement. Remember that this note will only be a zero or a one. Thus, by using sel 0 1, and only using the outlet for 1, we only pass to the rest of the algorithm when a chord is supposed to occur. We then have a counter that is for the current chord, modding that to 5 gives us an index for reading the progression table.

The output of tabread progression then in turn feeds four similar parallel algorithms that generate the specific notes of the given chord. These four algorithms are laid out left to right, and correspond to the root, third, fifth, and seventh of the given chord. In case of the root, the output of tabread progression and uses it as the input to tabread triads, which will yield the root of the triad. This is also added to one of two random octaves, 36 or 48 which will yield a note in the bass clef.

The other three notes add a number to the output of tabread progression. These numbers, one, two, and three, correspond to the third, fifth, and seventh of the chord. Modding that number by seven wraps any number that goes beyond the length of the table back to the beginning. The output of those expr statements then feeds tabread triads, yielding specific pitches. These pitches are added to one of three random octaves, 60, 72, or 84 to get random voicings. All four outputs of the expr statements, which give the transposed MIDI note numbers of the root, third, fifth, and seventh are fed to makenote which creates the chord when it is fed a velocity of 120. The output of this patch sounds like this . . .

Posted on

Pure Data: Chord Arpeggiator

In the previous post, we had an introduction to patches in Pure Data using a patch that plays a scale in quarter, eighth, and sixteenth notes in three different octaves. In this post we’ll be looking a way to generate diatonic triads using a chord progression. Again, these patches are intended to teach concepts of music theory along with concepts of music technology.

Some portions of this patch are similar to portions of the previous patch, so we’ll give them only a brief mention. For instance, the portion (in the upper left) that translates tempo (in this case 104 beats per minute) into time per beat (expressed in milliseconds) is essentially the same. Here is multiplied by .25 to yield a constant sixteenth note rhythm. Likewise, the portion of the patch that actually makes the notes and outputs them to MIDI (middle left) is essentially the same.

We have previously introduced loadbang and tables. Here we use tables to define diatonic triads in C Major. Using C as zero, triads 0 0 4 7 11 2 5 9 presents the notes of C major in stacked thirds (C, E, G, B, D, F, A respectively). If we pull out three consecutive numbers from this table, we will get a root, third, and fifth of a triad. We can wrap the table around to the beginning using modular mathematics (in this case mod seven) to yield thirds and fifths of the A chord, as well as the fifth of the F chord.

We can define a diatonic chord progression by noting the table position of the root of the chord in the triads table. Accordingly progression 0 0 2 6 5 gives us the roots C, G, A, and F. Given the layout of Major and minor thirds within a Major scale, this gives us the specific harmonies, C Major, G Major, A minor, and F Major. Fans of popular music will recognize this progression from numerous songs, including “Don’t Stop Believing,” “Can You Feel the Love Tonight,” and “Country Roads.”

The metronome used in the patch ticks off sixteenth note increments, so the % 64 object beneath the counter reduces the counter to a four measure sequence (four groups of 16 sixteenth notes adds up to 64 notes). This number is used in the object div 16, which yields the whole number portion (non-fractional portion) of the number being divided by 16. This will result in the values 0, 1, 2, or 3. This is essentially the current measure number in terms of the direction. Feeding this to tabread progression. Will give the index value for the root of that measure’s chord when used with the triads table.

The value from the tabread progression object is sent to the right inlet of the expr statement in the segment above. A random number between 0 and 2 inclusive is fed to the left inlet of the same expr statement. The random number represents whether the note created will be a root (0), a third (1), or a fifth (2). by adding these two values together we get the index of the specific pitch the triads table. Using mod 7, % 7 in the expr statement, insures that if we go beyond the end of the the triads table that we will wrap around the beginning of the table. This index is then passed to tabread triads, which returns the numeric value of the specified note.

Note that in the previous segment a second outlet from the number object beneath the expr statement is then sent to a bang. This activates the random code in the segment above, namely the selection of a random number between 0 and 2 inclusive. This number is passed to a sel statement, specifically, sel 0 1 2. This object activates one of the three leftmost outlets, depending upon whether it is passed a 0, 1, or 2 (respectively left to right). the rightmost outlet activates if anything besides 0, 1, or 2 is encountered. In this case we pass the three left most outlets to three messages, 60, 72, and 84. These numbers are three different octaves of C (middle C, C5, and C6 respectively). Those messages are fed to a number object, which in turn is fed to the right inlet of an expr statement. The left inlet of this expr statement comes from the output of tabread triads. Thus, in expr ($f1+$f2) the pitch is added to one of three octaves, yielding a random arpeggiation across three octaves of pitch space. Let’s listen to the results of this patch below.

Posted on

Pure Data: Scale Sequencer

Inspired by the book Learning Music Theory With Logic, Max, And Finale by Geoffrey Kidde, I have decided to revise my curriculum in my entry level theory course. However, rather than use Max, I’ve opted to teach Pure Data, due to its low price ($0). Pure Data is just different enough from Max that you can’t really use teaching materials for the two programs interchangeably. Thus, teaching Pure Data is forcing me to learn it, which is something I’ve wanted to do for quite a while. I hope to put up occasional posts that share Pure Data patches that I have developed for my teaching.

The first of these is a patch that plays major scales in three different octaves, at three different speeds.

Let’s look at this patch in a little detail. For those who are new to Pure Data, loadbang is used to run part of your patch when that patch is loaded. This loadbang routine sets up a table called scale, and defines the scale. Note that I’m using numbers of half steps to define a major scale (0 2 4 5 7 9 11 12). Notice as well that there is seemingly an extra 0 at the beginning. However, that first 0 indicates where in the table you begin loading material, so if we were to write this as text, we’d say begin at position 0 (the start of the table), and load in 0, 2, 4, 5, 7, 9, 11, and 12. This table data is included in a message object, and starts with a semicolon followed by a return character.  We would change the data in this message to change the mode or type of scale desired. If you want to update the patch after adding or changing information in the message that defines the scale, all you have to do is click on the message object when not in edit mode.

The following segment of the patch translates a tempo, measured in beats per minute to a time per beat measured in milliseconds. The equation expr (60/$f1)*1000 casts the number in the inlet (120) to a float. It divides 60 by that number, resulting in half a second. Multiplying that by 1000 translates that time per beat to milliseconds.

Directly beneath this segment there are three segments that instantiate metronomes at the quarter, eighth, and sixteenth note levels respectively. The quarter note metronome is passed the outlet of the time per beat. For the eighth notes, that same output is halved using expr (.5*$f1). Likewise, the sixteenth note durations result by multiplying by 1/4, using expr (.25*$f). In each case, a duration is also sent (dur1, dur2, dur3).

Below the metronomes are counters. The top two objects are very commonly used in Pure Data. The object on the left creates and stores a floating point number (a number with a decimal). To the right, we have an object that increments that number by adding one. This is accomplished by feeding the outlet of the float to the inlet of “+ 1”, and feeding the outlet of “+ 1” into the right inlet sets a new value for the float.

Since a scale has eight notes, any number higher than this is fairly useless for generating a scale. Thus, the outlet of float also feeds to “% 8”. The percentage sign means mod (modulus mathematics). Technically speaking, what is happening here is the number being fed to “% 8” is divided by eight, but the remainder of that division (the number that is left over in whole number division) is then sent to the outlet. This will result in a number between zero and seven.

This number is then used to generate both a pitch and a velocity. It is used as an index to select a value out of the the scale table, which is then added to a base pitch to determine the pitch range. The quarter notes use note number 36 as the base pitch. Since middle C (C4) in MIDI (Musical Instrument Digital Interface) is 60, 36 would be two octaves beneath middle C, otherwise known as C2, or Cello C. The eighth notes use middle C (60) as its base, and the sixteenth notes use two octaves above middle C (C6 or 84) as its base pitch. The pitch is then sent via the send command (s for short) using the variables note1, note2, and note3 for the quarters, eighths, and sixteenths respectively.

Key velocity in MIDI is a measurement of how quickly a key is pressed down. Traditionally it is used to indicate how loud a note is. That is a key that is pressed quickly will be louder than a key that is depressed slowly. MIDI is largely a seven bit system, so velocity values run between zero (which also can be used to turn a note off), and 127 (which is the loudest a note can be played). The equation expr (($f1*10)+50) results in having the notes get louder as the pitch of the scale goes up. For instance, when the index is zero, the velocity will be 50, and when the index is seven, the velocity will be 120.

These values, the notes (note1, note2, note3) and the velocities (vel1, vel2, vel3), are then sent to the output stage. The object makenote receives in its inlets (left to right) MIDI note number, velocity (0-127), and duration (in milliseconds). The outlets of makenote then feed the two leftmost inlets of noteout. The rightmost inlet of noteout receives a MIDI channel. The original specifications for MIDI, which was released in 1983, allow for 16 MIDI channels. Here, the notes are being sent on the first channel. Three different instances of makenote are being used here to allow different velocities and durations to be happening simultaneously.

You may check out this patch in action below using a piano sampler from Apple’s LogicPro to realize the sound.